Research Summary
Generalization of Kernel Regression and Wide Networks
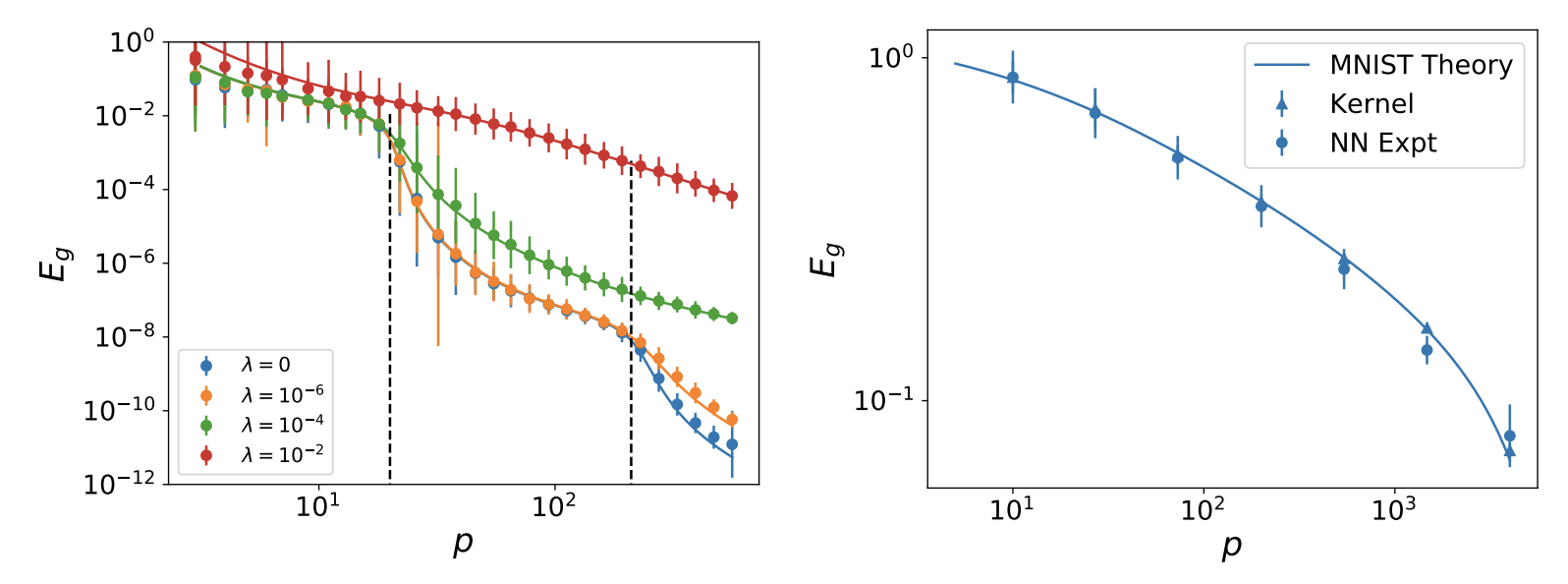
Attempting to gain analytical understanding of the inductive biases of neural networks and how their generalization performance varies with training sample size, I tried studying neural networks in the limit where they behave as linear functions of their parameters (NTK regime). Working with Abdul Canatar and Cengiz Pehlevan, we used the replica method from statistical physics to calculate expected test error for kernel regression models. We showed that the resulting theory accurately predicts learning curves for wide neural networks in the kernel regime. By solving a data-distribution dependent kernel eigenvalue problem, we showed that kernel eigenfunctions with large eigenvalues are estimated most rapidly as sample size increases. This theory provided a notion of inductive bias for kernel regression, defining what kinds of tasks can be learned most quickly for a given kernel and data distribution.
Dynamical Model of Neural Scaling Laws
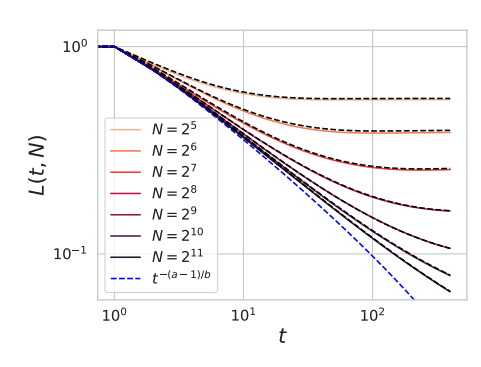
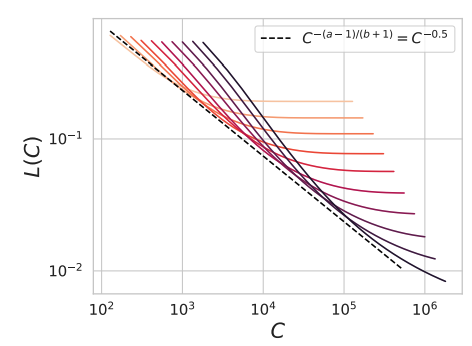
Recently I extended this kernel generalization model with Alex Atanasov and Cengiz Pehlevan to study gradient descent dynamics and finite width. The resulting theory can be used to derive compute optimal scaling laws where model size and training time can be chosen optimally under a compute budget.
Dynamical Field Theory for Wide Feature Learning Neural Networks
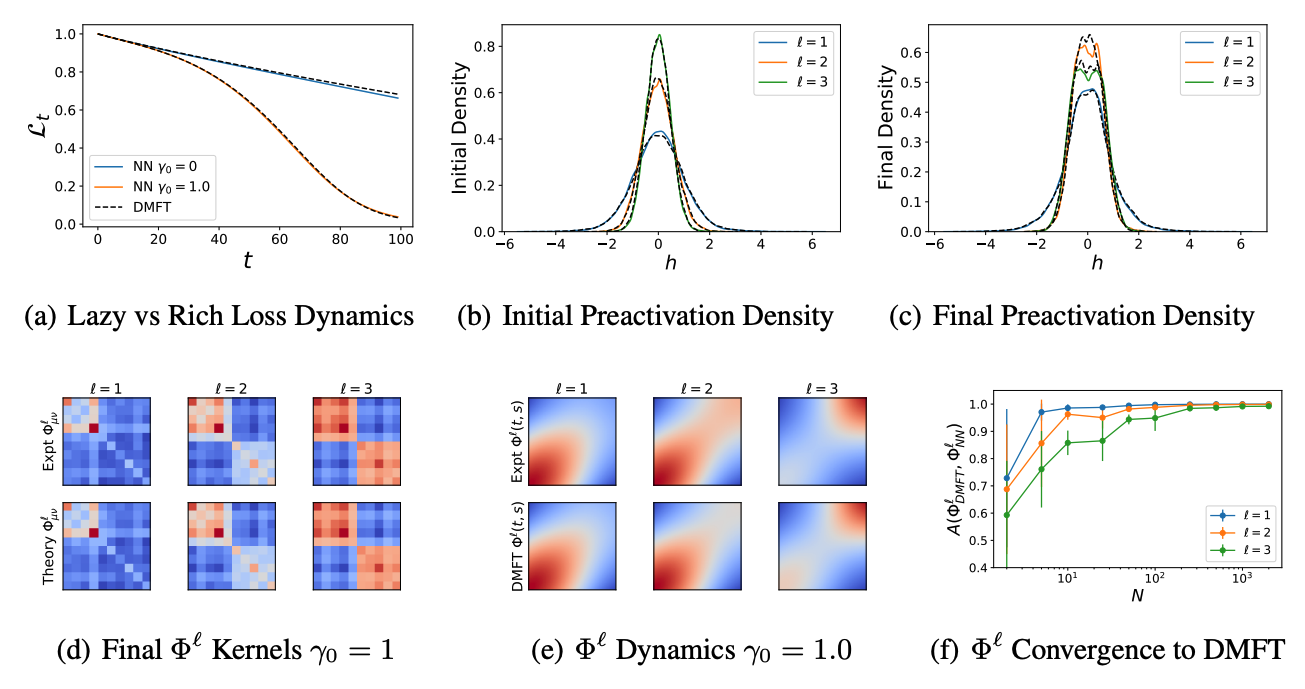
Dynamical mean field theory (DMFT) is a heuristic physics method for computing autocorrelation functions of high dimensional disordered dynamical systems. Using this method, we derive self-consistent equations for the evolution of a neural network’s neural tangent kernel and give a numerical procedure to approximately solve the dynamics. We study these dynamics across different richness scales \(\gamma_0\) which quantify the amount of feature learning performed during training.
Learning Dynamics in Large Width and Depth Limits: Depthwise Hyperparameter Transfer
With Lorenzo Noci, Mufan Bill Li, Boris Hanin and Cengiz Pehlevan, we studied large depth residual networks and their dynamics at infinite width and depth. Ordinary parameterizations of ResNets do not achieve consistent dependence on hyperparameters across depths, but we showed that under a certain scaling of the parameters and learning rates, the network can exhibit consistent optimal hyperparameters across both widths and depths.
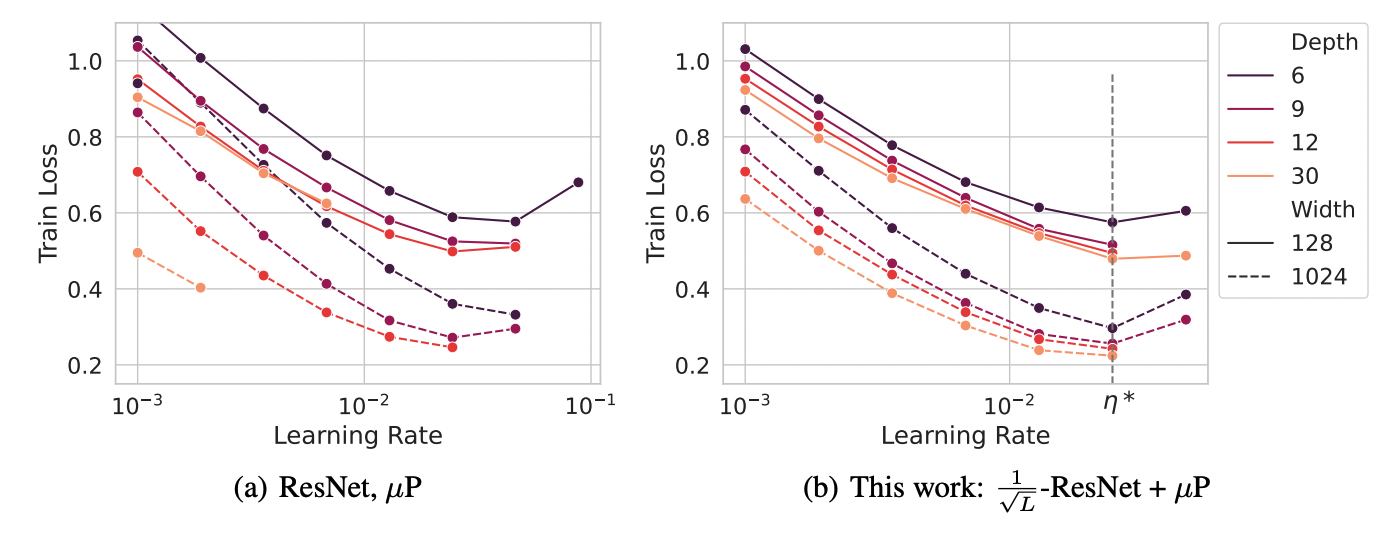
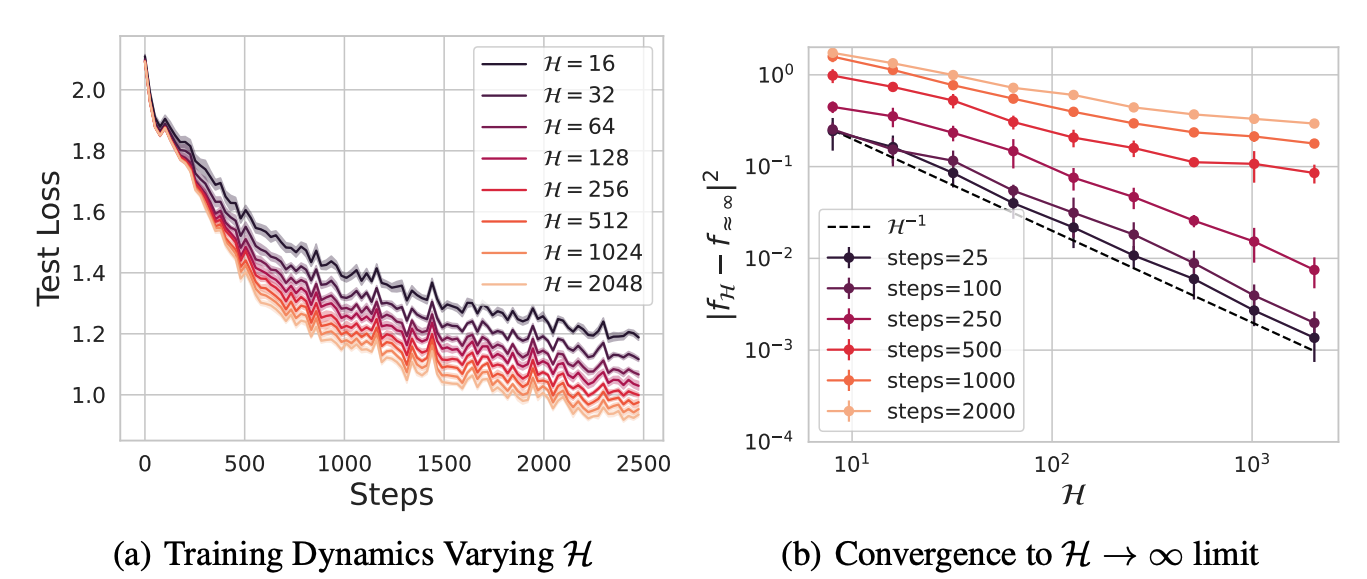
We also used DMFT methods to analyze the asymptotic convergence to the limiting dynamics. The convergence in width and depth commute for any finite training times.
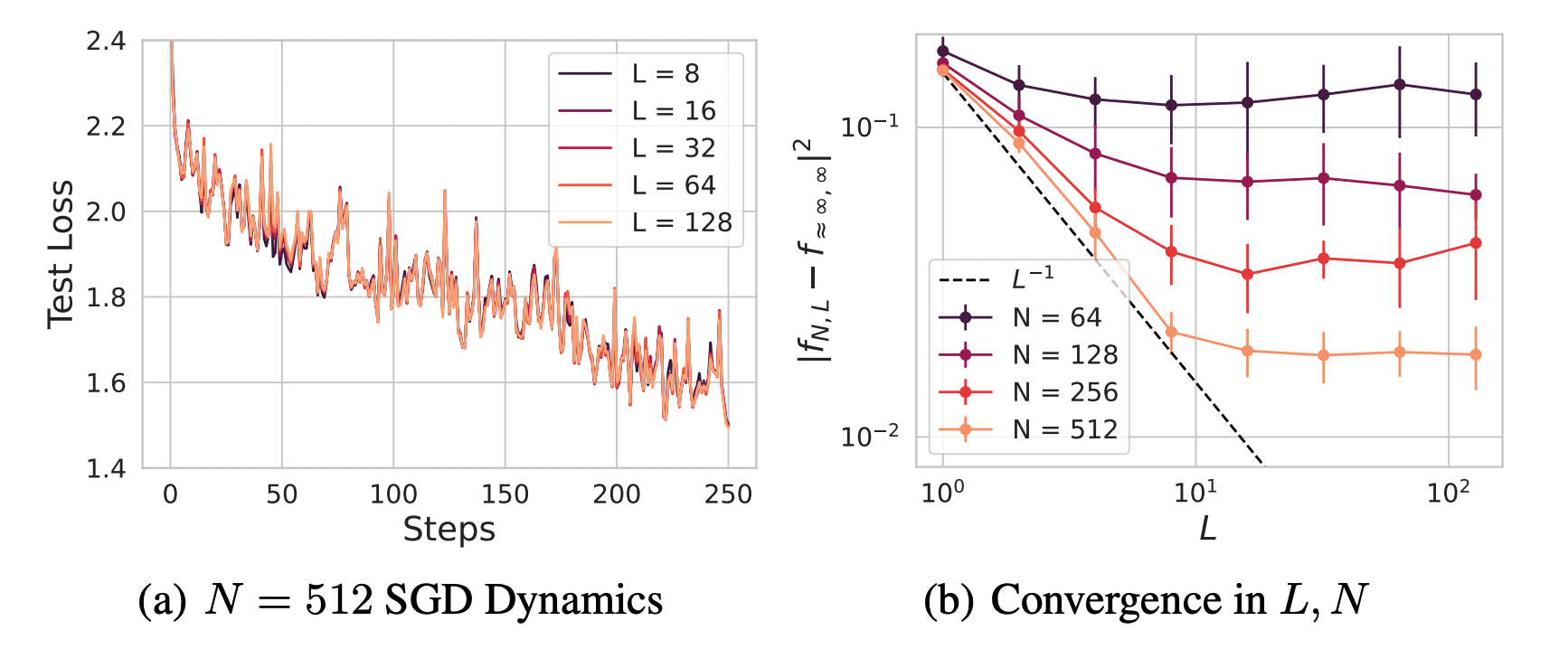
Infinite Width, Head and Depth Limits of Transformers
With Hamza Chadhry and Cengiz Pehlevan, I worked out similar DMFT limits for transformer models with self attention layers. We identified different ways of taking infinite limits including taking the dimension per head to infinity or the number of heads to infinity. We showed that the infinite dimension per head limits causes attention heads to collapse to the same dynamics, while the infinite head limit maintains diversity across attention heads. We also investigate different types of infinite depth limits in these models.
Loss Dynamics of Temporal Difference Reinforcement Learning
With Paul Masset, Henry Kuo and Cengiz Pehlevan we studied how the structure of feature maps, policy, learning rate, discount factor all influence the learning dynamics of value estimation in high dimensions.
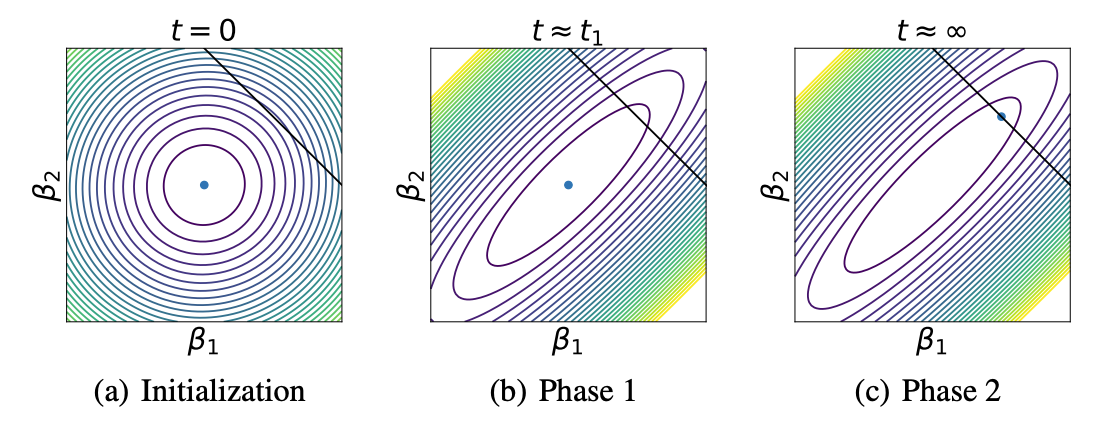
Kernel Alignment
With Alex Atanasov, I studied how networks from small initialization could still effectively be kernel machines but with a kernel that has adapted to the statistics of the training data. We realized that if the kernel adapts to the data early on while small in overall scale, then the neural network will essentially be a kernel regression solution with that final kernel. We call this phenomenon silent alignment and illustrate it below by plotting RKHS norm for a deep linear NTK over the space of linear functions \(\beta\).
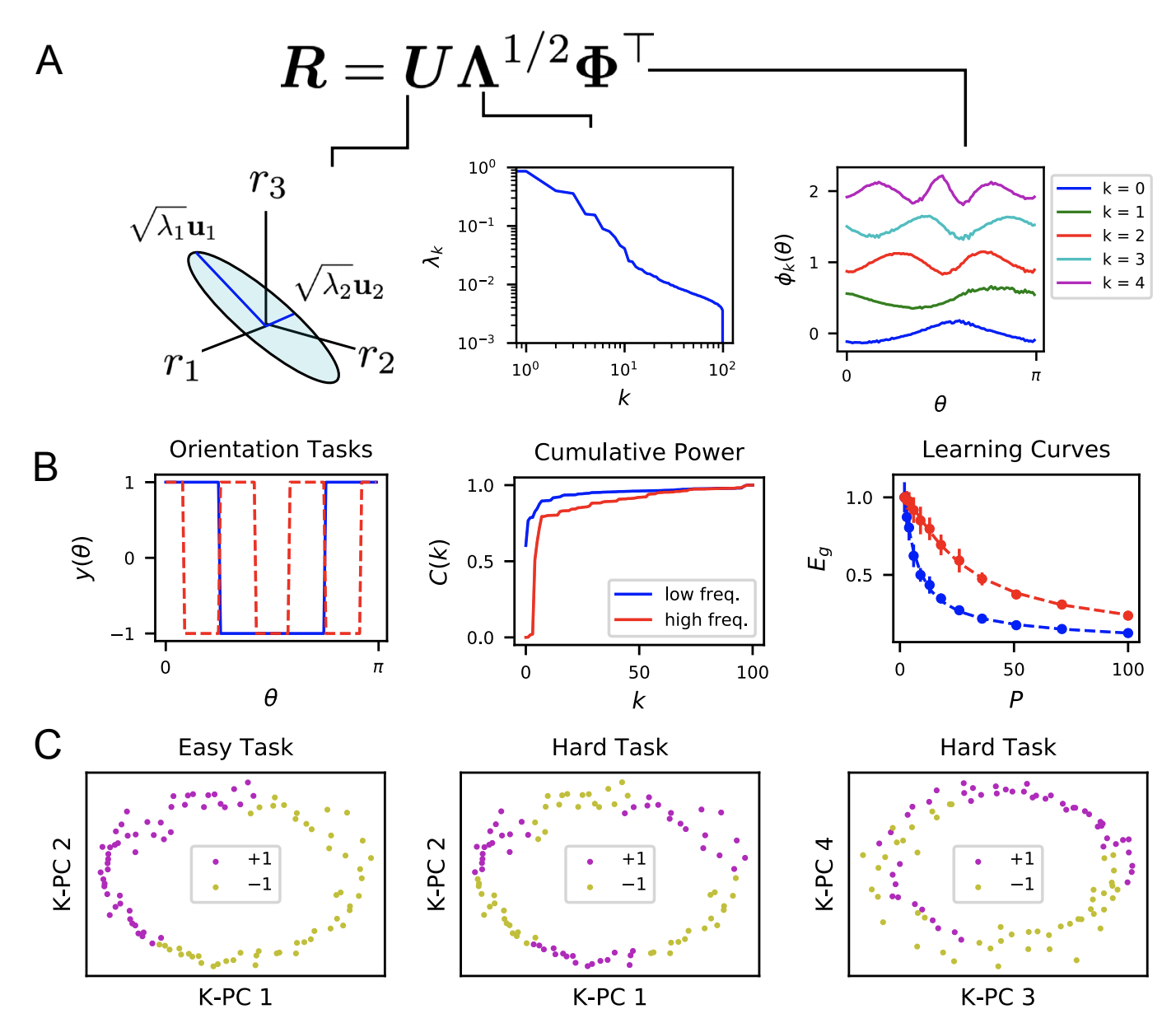
The Structure of Neural Codes Alters Inductive Bias
I am also interested in using learning theory ideas such as sample efficiency to help understand how the brain learns from experience. We use our theory of generalization to study what kinds of associations are easy or hard for visual cortex to learn from a limited number of examples. We also apply our model to predict learning curves for readouts from RNNs.
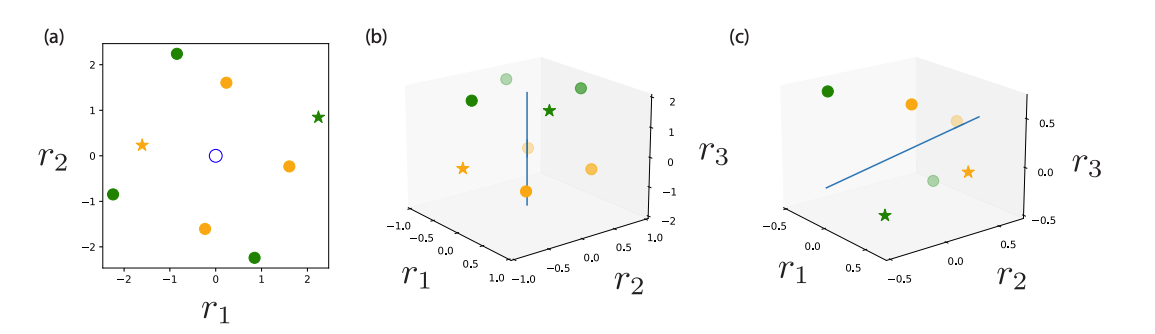
Capacity of Group Equivariant Neural Codes
With Matthew Farrell, we calculated the capacity of linear readouts from group equivariant neural codes. Concretely, for a group G, we quantify the fraction of random binary labelings of G orbits in an equivariant neural space which are linearly separable. While the traditional capacity, given by Cover’s function counting theorem, states that the fraction of separable dichotomies is approximately 1 provided that the number of points is smaller than the dimension of the code, our result demonstrated that the G-invariant capacity problem only depends on the number of trivial irreducible representations (dimension of the fixed-point subspace). Below is an example of 2 orbits of \(Z_4\) in three dimensions which can only be separated along the one trivial dimension.
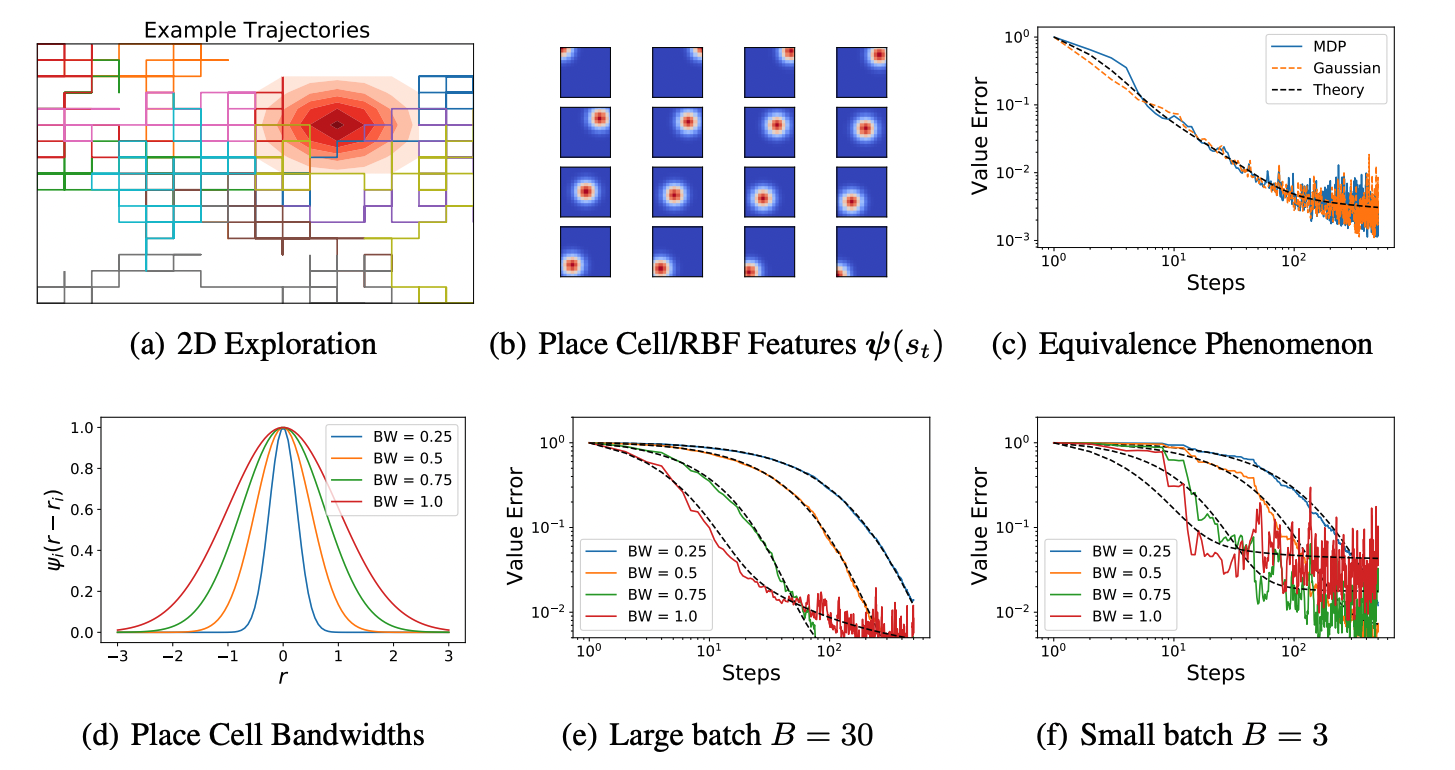
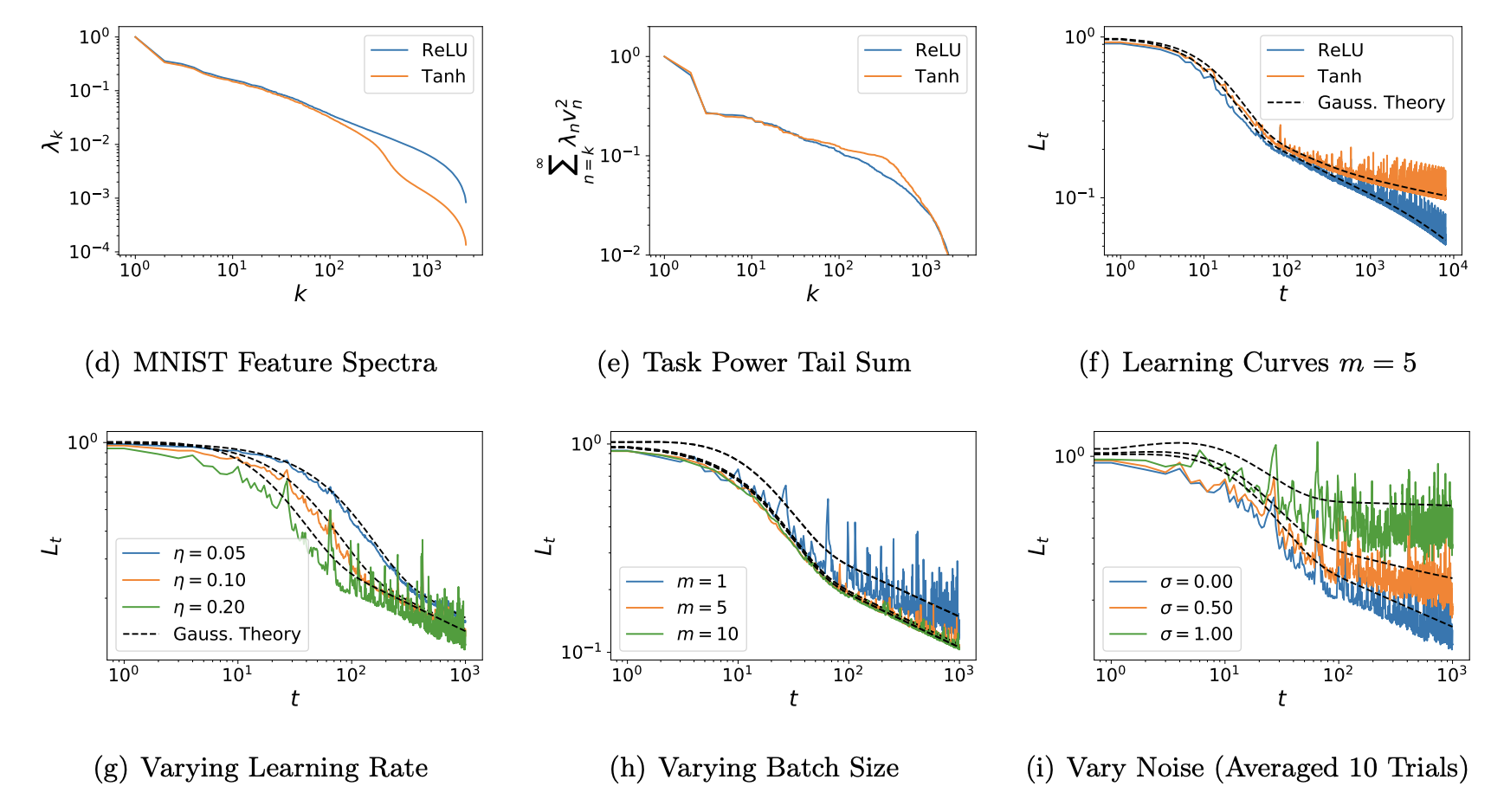
Test Error Dynamics during SGD on Structured Feature Maps
I recently analyzed the expected test loss of SGD by averaging over the history of samples for linear readouts from structured feature maps. The test error can be closed in terms of second and fourth moments of the features and, under certain conditions, the test error predicted by Gaussian features with structured correlations accurately predicts the test loss. We show that errors for different eigenmodes are in general coupled but decouple when learning rate is small and batch size is large. I used the theory to extract test loss scalings of wide conv nets and wide MLPs and show that the theory can predict the better power law exponent for conv-nets on CIFAR-10. The theory also shows that there can be an optimal batch size to minimize expected test error if the compute budget is fixed.
Out of Distribution Test Error
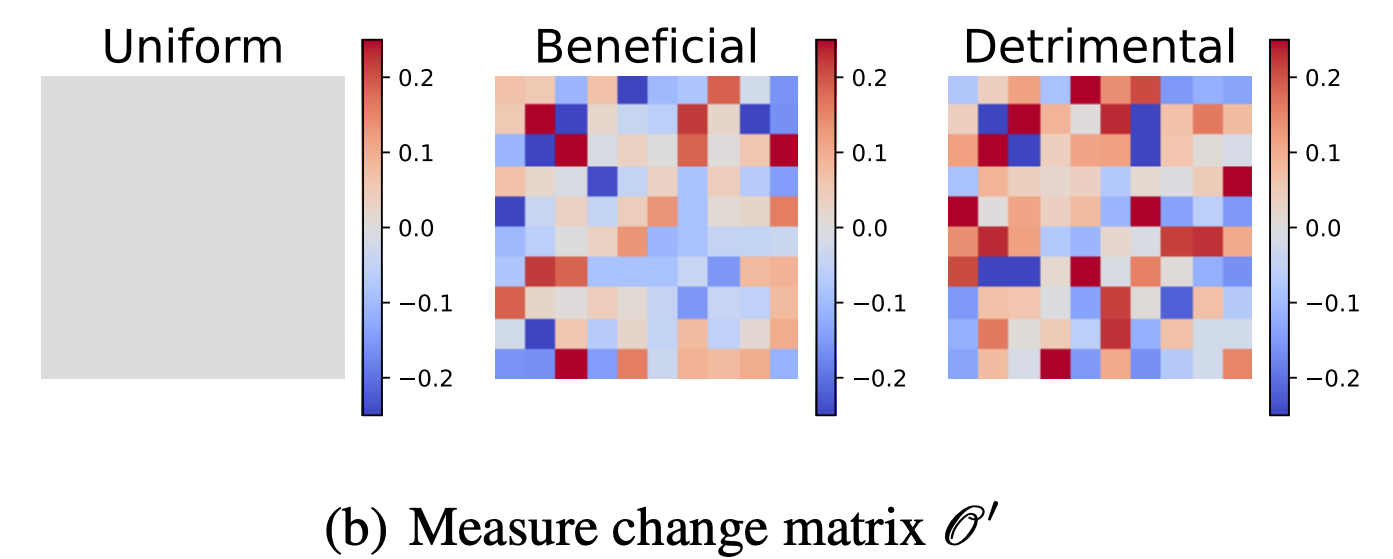
Abdulkadir Canatar and I calculated how kernels (and wide NNs) perform under distribution shift, when test and training distributions do not match. The theory relies heavily on an overlap matrix which measures overlaps of train-distribution eigenfunctions over the test measure. Using our theory, we developed an algorithm to optimize the training measure for a fixed learning problem to get a lower expected test error. We find that the optimal training measure is often different than the test measure. We also used gradient descent on our theoretical expressions to identify beneficial and adversarial test measures for a fixed training distribution. We show that our theory accurately captures generalization under distribution shift for kernel methods and wide neural networks.
Feature Learning and its Impact on Training Speed
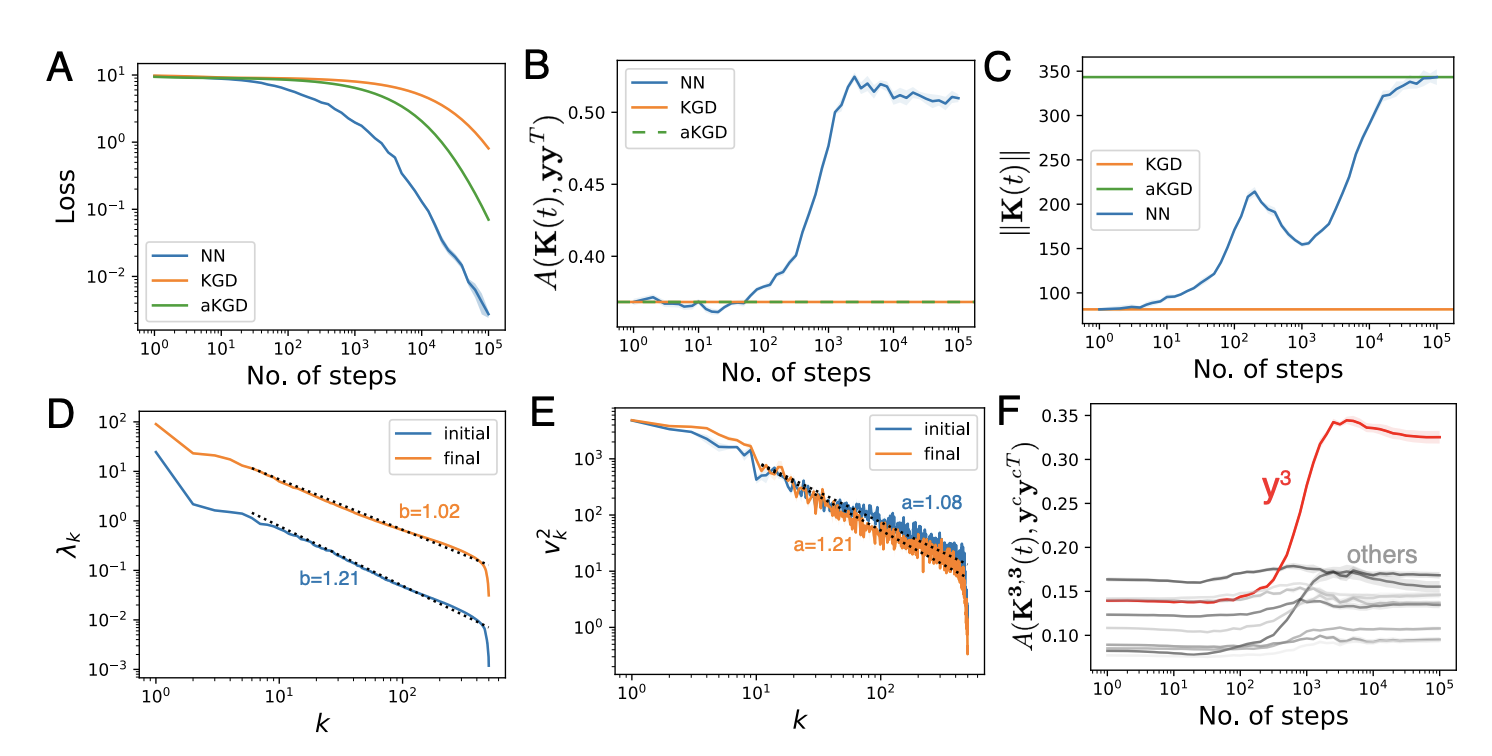
Haozhe Shan and I studied both experimentally and with toy models, how the parameter dependent neural tangent kernel aligns with the training data during optimization. Of particular interest was how the evolution of features influenced the loss dynamics. Experiments showed that the kernel becomes aligned with the outer product of labels, though not perfectly. We developed a toy model where features evolve to minimize the predicted loss in the next time step. In this model, the features and the errors evolve in a coupled elliptical system. The theory reproduces the experimental finding of an additive update to the kernel which is the outer product of labels.